KESEBANGUNAN DAN KEKONGRUENAN: SOAL DAN PEMBAHSAN JILID II

Perhatikan gambar dua buah belah ketupat di bawah ini, apakah kedua bangun tersebut dapat dinyatakan kongruen?

Penyelesaian:

Untuk menjawab soal tersebut, kalian harus mengingat kembali akan sifat-sifat bangun datar yang dimiliki oleh belah ketupat, yaitu:

a. Semua sisi sama panjang dan sepasang-sepasang sejajar.

b. sudut-sudut yang berhadapan sama besar dan terbagi dua sama besar.

Pada belah ketupat ABCD diatas, diketahui bahwa AB = BC = CD = AD = 6 cm,

Sudut A = sudut C = 40⁰, dan sudut B = sudut D = 140⁰ (sudut-sudut yang berhadapan)

Pada belah ketupat EFGH diatas, diketahui bahwa EF = FG = GH = EH = 6 cm,

Sudut E = sudut G = 40⁰, dan sudut F = sudut H = 140⁰

Dari uraian tersebut dapat diperoleh:

AB/EF = BC/FG = CD/GF = AD=EH = 1

sudut A = sudut C = Sudut E = sudut G = 40⁰

sudut B = sudut D = sudut F = sudut H = 140⁰

Karena sisi-sisinya yang bersesuaian memiliki ukuran sama panjang serta sudut-sudut yang bersesuaian sama besarnya, maka bangun ABCD dan EFGH bisa dikatakan kongruen.
Perhatikan gambar layang-layang di bawah ini:

Apakah layang-layang ABCD dan EFGH sebangun?

Penyelesaian:

Layang-layang mempunyai sepasang sudut berhadapan yang sama besar. Sifat tersebut dapat kita gunakan untuk mencari sudut-sudut yang belum diketahui besarnya pada sebuah laying-layang.

Untuk layang-layang ABCD:

Sudut D = Sudut B = 110⁰ dan sudut A = 60⁰

maka sudut C = 360⁰ – (110 + 110 + 80)⁰ = 80⁰

Untuk layang-layang EFGH:

Sudut H = Sudut F = 110⁰ dan sudut G = 80⁰

maka sudut E = 360⁰ – (110 + 110 + 80)⁰ = 60⁰

Dengan demikian kita bisa menyimpulkan bahwa:

Sudut A = sudut E, sudut B = sudut F, sudut C = sudut G, dan sudut D = sudut H. dan ternyata sudut-sudut yang bersesuaian pada kedua laying-layang tersebut sama besar.

Untuk layang-layang ABCD, diketahui bahwa CD = BC = 6 cm dan AB = AD = 9 cm

Untuk layang-layang EFGH, diketahui bahwa GH = FG = 4 cm dan EH = EF = 6 cm

Sehingga dapat diperoleh:

BC/FG = DC/GH = 6/4 = 3/2

AD/EH = AB/EF = 9/6 = 3/2

Karena sudut-sudutnya sama besar dan perbandingan sisi-sisinya bersesuaian maka dapat kita simpulkan bahwa laying-layang ABCD bersifat sebangun dengan EFGH.
Pada peta berskala 1:2.100.000, diketahui jarak antara Ambon dan Liang 2,1 cm. Tentukan jarak sebenarnya!
Penyelesaian:
Pada soal kita ketahui:
Skala = 1:2.100.00
Ukuran pada peta = 2,1 cm
Kita diminta mencari jarak sebenarnya.
Jawab:
Jarak sebenarnya = Ukuran pada peta : skala
        = 2,1 cm : 1/2.100.000
        = 2,1 cm x 2.100.000/1
        = 4.410.000 cm
        = 44,1 km
Dua persegi panjang berturut-turut berukuran 20cm x 15cm dan 4cm x 3cm. Apakah keduanya sebangun?
Penyelesaian:
Panjang 1 : panjang 2 = 20cm : 4cm = 5
lebar 1 : lebar 2 = 15cm : 3cm = 5
Oleh karena sudut-sudut yang bersesuaian sama besar dan panjang sisi-sisi yang bersesuaian sebanding, maka kedua persegi tersebut sebangun.
Perhatikan gambar berikut:

Apakah jajargenjang ABCD dan PGRS kongruen?
Penyelesaian:
Sisi-sisi yang bersesuaian sama panjang.
AB = QR = 2cm dan CD = PS = 2cm
AD = PQ = 3cm dan BC = SR = 3cm
Sudut-sudut yang bersesuaian sama besar.
<A = <S dan <C = <Q
<B = <P dan <D = <R
Jadi, jajargenjang ABCD dan PQRS kongruen.
Gambar di bawah ini menunjukkan dua bangun datar yang sebangun.

Hitunglah:
a. panjang AB
b. panjang PS
Penyelesaian:
Oleh karena bangun ABCD dan PGRS sebangun, maka panjang sisi-sisi yang bersesuain sebanding.
a. AB/PQ = DC/SR
   AB/16 = 6/12
   AB.12 = 16.6
   12AB = 96
   AB    = 96:12
   AB    = 8cm
Jadi panjang AB = 8cm

b. PS/AD = SR/DC
   PS/4 = 12/6
   PS.6 = 12.4
   6PS   = 48
   PS    = 48:6
   PS    = 8cm
Jadi, panjang PS = 8cm
Perhatikan gambar berikut:

Trapesium ABCD sebangun dengan trapesium EFGH. Panjang EH adalah...
Penyelesaian:
Oleh karena bangun ABCD dan EFGH sebangun, maka panjang sisi-sisi yang bersesuaian memiliki perbandingan yang sama.
EH/AD = EF/AB
EH/8 = 18/12
EH.12 = 8.18
12EH = 144
EH    = 144:12
EH    = 12cm
Jadi, panjang EH adalah 12cm

Soal 6:
Kedua jajargenjang di bawah ini sebangun. Panjang BC adalah....

Penyelesaian:
Oleh karena bangun ABCD dan EFGH sebangun, maka panjang sisi-sisi yang bersesuaian memiliki perbandingan yang sama.
BC/EH = AB/EF
BC/4 = 9/6
BC.6 = 4.9
6BC   = 36
BC    = 36:6
BC    = 6cm
Jadi, panjang BC adalah 6cm.
Perhatikan gambar segitiga dibawah ini!

Panjang AB adalah...
A. 20 cm
B. 40 cm
C. 80 cm
D. 100 cm

Pembahasan
AB : BC = AD : DE
AB : 20 cm = 20 cm : 5 cm
AB : 20 cm = 4
AB = 4 x 20 cm = 80 cm
Jawaban: C
Perhatikan gambar!

Jika AB = 12 cm, CD = 7 cm, AD = 8 cm, dan DE = 8 cm maka panjang CE adalah....
A. 16 cm
B. 8 cm
C. 7 cm
D. 6 cm

Pembahasan
AB : BC = DE : CE
12 cm : (AD + CE) = 8 cm : CE
3 : (8 cm + CE) = 2 : CE
3/2 = (8 cm + CE) / CE
3/2 = 8 cm / CE + CE / CE
3/2 = 8 cm / CE + 1
8 cm / CE = 3/2 - 1 = 1/2
CE = 8 cm / (1/2) = 16 cm
Jawaban: A
Perhatikan gambar dibawah ini!

Panjang DE = ...
A. 4 cm
B. 9 cm
C. 12 cm
D. 15 cm

Pembahasan
AB : AC = DE : CD
3 cm : 4 cm = DE : 12 cm
DE = 3/4 x 12 cm = 9 cm
Jawaban: B
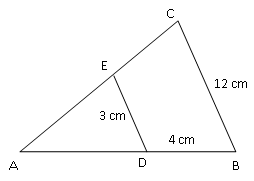
Panjang AD adalah...
A. 4/3 cm
B. 5/3 cm
C. 1 cm
D. 2 cm

Pembahasan
BC : AB = DE : AD
12 cm : (AD + DB) = 3 cm : AD
12 cm : (AD + 4 cm) = 3 cm : AD
(AD + 4 cm) / AD = 12 cm / 3 cm = 4 cm
AD / AD + 4 cm / AD = 4 cm
1 + 4 cm / AD = 4 cm
4 cm / AD = 4 - 1 = 3 cm
AD = 4/3 cm
Jawaban: A
Sebuah karton berukutan 30 cm x 20 cm. Andi menempelkan gambar berwarna pada karton tersebut sehingga sisa karton disebelah kiri, kanan, dan atas gambar adalah 2 cm. Jika karton dan gambar sebangun, sisa karton bagian bawah selebar...
A. 2 cm
B. 4 cm
C. 6 cm
D. 8 cm

Pembahasan

Karena sebangun, sehingga
Panjang karton : lebar karton = panjang gambar : lebar gambar
30 cm : 20 cm = (30 - 2 - x) cm : (20 - 2 - 2) cm
3/2 = (28 - x) cm : 16 cm
(28 - x) cm = 3/2 x 16 cm = 24 cm
x = 28 cm - 24 cm = 4 cm
Jawaban: B

KESEBANGUNAN DAN KEKONGRUENAN

Kamis, 22 September 2016

SOAL DAN PEMBAHSAN JILID II

Penyelesaian:

Penyelesaian:

Tidak ada komentar:

Posting Komentar