SOAL DAN PEMBAHASAN JILID 1

1. Diberikan dua buah persegipanjang ABCD dan persegipanjang PQRS seperti gambar berikut.
   
   Kedua persegipanjang tersebut adalah sebangun. Tentukan:
   a) panjang PQ
   b) luas dan keliling persegipanjang PQRS Pembahasan
   a) Perbandingan panjang garis AB dengan AD bersesuaian dengan perbandingan panjang garis PQ dengan PS. Sehingga
   Panjang PQ = 24 cm
   
   b) Luas persegipanjang PQRS = PQ x PS = 24 cm x 6 cm = 144 cm²
   Keliling persegipanjang PQRS = 2 x (PQ + PS) = 2 x (24 cm + 6 cm) = 60 cm
2.  Perhatikan gambar berikut!
   Tentukan panjang DB!
   Pembahasan
   Soal ini tentang kesebangunan segitiga. Segitiga ABC yang lebih besar sebangun dengan segitiga kecil ADE sehingga perbandingan panjang sisi-sisi yang bersesuaian akan sama. Temukan dulu panjang sisi AB, ambil perbandingan alas dan tinggi dari kedua segitiga seperti berikut ini:
   
   Dengan demikian DB = AB − AD = 15 cm − 10 cm = 5 cm
   
   
3.  Dari soal berikut, tentukan:
   
   a) QR
   b) QU
   Pembahasan
   a) Penyelesaian seperti nomor 2, ambil perbandingan sisi-sisi yang bersesuaian dari segitiga PQR dan segitiga SUR.
   b) QU = QR − UR = 20 cm − 15 cm = 5 cm
   
   
4.  Perhatikan gambar berikut!
   Tentukan panjang DE
   Pembahasan
   Kesebangunan dua segitiga siku-siku
   
   
5.  Dari soal berikut tentukan panjang DE!
   Pembahasan
   Bedakan pengambilan sisi-sisi yang bersesuaian dari soal nomor sebelumnya.
   
   
6.  Diketahui panjang SR adalah 8 cm.
   Tentukan panjang QS!
   Pembahasan
   Kongruensi dua segitiga siku-siku, tentukan lebih dahulu panjang PS gunakan teorema phytagoras akan didapat angka 6 cm untuk panjang PS. Kemudian lakukan perbandingan sisi yang sesuai:
   
   
7.  Dari soal berikut ini tentukan panjang EF!
   Pembahasan
   Buat satu garis yang sejajar dengan garis AD namakan CH seperti gambar berikut.
   Terlihat muncul  data-data baru yaitu EG = 15 cm, AH = 15 cm dan HB = 13 cm. Ambil dua segitiga sebangun GFC dan HBC bandingkan sisi-sisi yang bersesuaian:
   Dengan demikian panjang EF = EG + GF = 15 + 4 = 19 cm
   
   
8.  Perhatikan gambar berikut ini.
   
   Tentukan panjang EF, jika titik E dan titik F berturut-turut adalah titik tengah diagonal DB dan diagonal CA!
   Pembahasan Cara pertama, Perhatikan garis DB yang dibagi menjadi segmen-segmen DE, EG dan GB.
   Misalkan
   panjang DB adalah 2a
   maka
   DE = a
   EB = a
   Dari kesebangunan segitiga DGC dan segitiga AGB didapatkan perbandingan panjang garis
   DG : GB = 2 : 1  didapatnya  dari 24 cm : 12 cm
   
   Sehingga
   
   
   Dari pembagian segmen garis DB terlihat bahwa
   DG = DE + GE
   Sehingga
   
   
   Akhirnya bandingkan sisi-sisi yang bersesuaian pada segitiga kongruen ABG dan EGF.
   Cara kedua,  namun diingat hanya untuk tipe soal seperti ini saja, jadi titik E dan F nya di tengah-tengah, jangan gunakan untuk tipe soal yang lain:
   
   
   
   
9.  Perhatikan gambar berikut ini!
   
   
   Jarak titik E ke B adalah....
   A. 1,5
   B. 6
   C. 8
   D. 10
   Pembahasan
   Misalkan EB dinamakan x, maka AB nantinya akan sama dengan (2 + x). Perbandingan sisi EB dengan ED pada segitiga kecil (segitiga BDE), harus sama dengan perbandingan AB dengan AC pada segitiga besar (segitiga BCA). Selanjutnya:
   
   Jadi panjang EB adalah 6 cm.
   
   
10.  Perhatikan gambar berikut ini!
    
    
    Panjang TQ adalah...
    A. 4
    B. 5
    C. 6
    D. 7
    (UN 2007)
    Pembahasan
    Dengan cara yang sama dengan nomor 9 diperoleh:
    
    
    
11.  Sebuah karton berukuran tinggi 30 cm dan lebar 20 cm. Budi menempelkan sebuah foto sehingga sisa karton di sebelah kiri, kanan, atas foto adalah 2 cm.
    Jika foto dan karton sebangun, sisa karton di bawah foto adalah...
    A. 5 cm
    B. 4 cm
    C. 3 cm
    D. 2 cm
    (Modifikasi Soal Kesebangunan - UN 2010)
    Pembahasan
    Perhatikan ilustrasi foto dan karton tempat menempel berikut, misalkan sisa panjang karton namakan sebagai x.
    
    
    Perbandingan panjang dengan lebar foto harus sama dengan perbandingan panjang dengan lebar dari karton, karena sebangun.
    
    
    
    
12.  Sebuah foto berukuran tinggi 30 cm dan lebar 20 cm ditempel pada sebuah karton. Sisa karton di sebelah kiri, kanan, atas foto 2 cm. Jika foto dan karton sebangun, sisa karton di bawah foto adalah...
    A. 5 cm
    B. 4 cm
    C. 3 cm
    D. 2 cm
    (Soal Kesebangunan - Soal UN Matematika 2010)
    Pembahasan
    Perhatikan ilustrasi foto dan karton tempat menempel berikut,
    
    
    Perbandingan panjang dengan lebar foto harus sama dengan perbandingan panjang dengan lebar dari karton, karena sebangun. Perhatikan perbedaannya dengan nomor sebelumnya dalam menempatkan x.
    
    
    
    
13.  Perhatikan gambar!
    
    
    Panjang EF adalah...
    A. 20 cm
    B. 21 cm
    C. 23 cm
    D. 26 cm
    (UN SMP 2013)
    Pembahasan
    Tambahaan garis bantu, beri nama BG.
    
    
    Panjang DG jadi 14 cm, dan GC 21 cm karena tadinya DC = 35 cm. Bandingkan sisi segitiga besar BGC dan segitiga kecil BHF yang bersesuaian hingga diperoleh panjang HF dulu.
    
    
    
14.  Perhatikan gambar di samping!
    
    Panjang TR adalah….
    A. 2 cm
    B. 3 cm
    C. 4 cm
    D. 6 cm
    (UN Matematika SMP/MTs tahun 2014) Pembahasan
    Dicoba dulu, petunjuknya, ΔPQR sebangun dengan ΔPTS, dengan ∠T bersesuaian dengan ∠Q, dan ∠S bersesuaian dengan ∠R. Sementara ∠P sama-sama dipakai kedua segitiga. Bandingkan sisi-sisi yang diketahui dan bersesuaian, biar lebih mudah diliat bisa digambar dulu kedua segitiga secara terpisah.
    
    
    
    
15.  Kesebangunan Dua Persegi Panjang Psersegi panjang ABCD memiliki panjang dan lebar secara berturut-turut 13 cm dan 39 cm. Jika persegi panjang ABCD tersebut sebangun dengan persegi panjang KLMN, yang sisi terpanjangnya memiliki ukuran 24 cm, tentukan panjang sisi terpendek dari persegi panjang KLMN.
    Pembahasan Persegi panjang ABCD dan KLMN dapat digambarkan sebagai berikut.
    
    Karena persegi panjang ABCD sebangun dengan KLMN, maka panjang sisi-sisi yang bersesuaian dari kedua persegi panjang tersebut merupakan perbandingan yang senilai. Sehingga,
    
    Jadi, panjang sisi terpendek dari persegi panjang KLMN adalah 8 cm.
16.  Perhatikan gambar di bawah ini!
    
    Jika diketahui AB = 144 cm dan BC = 108 cm, persegi panjang ABCD, BCGF, dan EHGD merupakan persegi panjang-persegi panjang yang sebangun, tentukan luas daerah AFHE!
    Pembahasan Karena persegi panjang ABCD sebangun dengan persegi panjang BCGF, maka
    
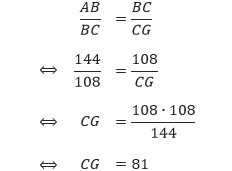
    Karena CD = AB = 144 cm dan CG = 81 cm, maka EH = GD = CD – CG = 144 – 81 = 63 cm. Diketahui ABCD juga sebangun dengan EHGD, maka didapatkan
    
    Sehingga, FH = FG – HG = BC – HG = 108 – 47,75 = 60,25 cm. Diperoleh luas dari segi empat AFHE adalah EH × FH = 63 × 60,25 = 3.795,75 cm².