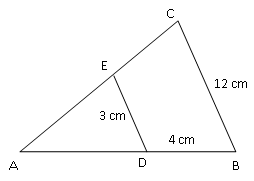
Sebutkan benda-benda
di sekitarmu yang
mempunyai bentuk
sama!
2. Sebutkan benda-benda
di sekitarmu yang
mempunyai bentuk sama
tetapi ukuran berbeda!
3. Sebutkan benda-benda
di sekitarmu yang
mempunyai bentuk dan
ukuran sama!
di sekitarmu yang
mempunyai bentuk
sama!
2. Sebutkan benda-benda
di sekitarmu yang
mempunyai bentuk sama
tetapi ukuran berbeda!
3. Sebutkan benda-benda
di sekitarmu yang
mempunyai bentuk dan
ukuran sama!